統計学を学んでいると「統計的仮説検定」に出会うでしょう。
筆者は難しくてよくわからないなと感じていましたが、皆さんはいかがでしょうか?
本記事では筆者が学んで理解した「統計的仮説検定」を筆者の言葉で説明します!
この記事を読めば、「仮説検定とは何か」「有意水準とは何か」ということが理解できます。
仮説検定の「仮説」
「仮説検定」とは何か。筆者の人生のモットーを表す四字熟語ではありません。
「仮説検定」は「仮説」と「検定」に分解できます。統計学において「仮説」と「検定」が意味する手続きはそれぞれ異なります。まずは「仮説」について深掘りしましょう!
一般的に、「仮説」とは現象を説明するために立てられる主張のことです。
たとえば、諸外国と比較して日本人の平均寿命は長いという現象を考えてみましょう。この現象の背後にある要因として「日本の医療制度が優れていること」や「日本の食文化が健康的なこと」のような説明が挙げられます。このような説が「仮説」なのです。
統計学においても同様です。統計学における「仮説」とは「統計的問題」に対する「主張」のこと。
この「仮説」を導くためには、仮説によって説明される「統計的問題」を明確にする必要があります。問題に対して「仮説」を突きつけるのだから。まずは「統計的問題」を設定してみましょう!
確率変数\(X_1, \cdots, X_n\)が、パラメータ\( \theta \)による確率(密度)関数\( f(x | \theta) \)で与えられる分布に独立に従うとしましょう。
$$ X_1, \cdots, X_n \overset{\text{i.i.d.}}{\sim} f(x | \theta) $$
確率変数の分布を定めるパラメータ\( \theta \)は未知の値。ですから、この確率分布から得られたデータをもとにパラメータに関する仮説を立てるのです。「パラメータ\( \theta \)はこの値に等しい!」とか「パラメータ\( \theta \)はこの範囲にある!」のように。このような主張が統計学における「仮説」の正体なのです。
ここでは、「パラメータが取り得る値の範囲全体を表すパラメータ空間\( \Theta \)における部分集合\( \Theta_0 \subset \Theta \)に\( \theta \)が属する」を仮説としましょう。このような仮説は(「検定」によって否定されることが多く)帰無仮説(きむかせつ:null hypothesis)と呼ばれ、\( H_0 \)という記号で表されます。

帰無仮説「\( H_0\ : \ \theta \in \Theta_0 \)」
一方、「部分集合\( \Theta_0 \)以外の空間(\( \Theta \)から\( \Theta_0 \)を除いた空間)に\( \theta \)が属する」という、帰無仮説とは反対を主張する仮説も考えられます。このような仮説は対立仮説(たいりつかせつ:alternative hypothesis)と呼ばれ、\( H_1 \)という記号で表されます。

対立仮説「\( H_1\ : \ \theta \in \Theta \backslash \Theta_0 \)」
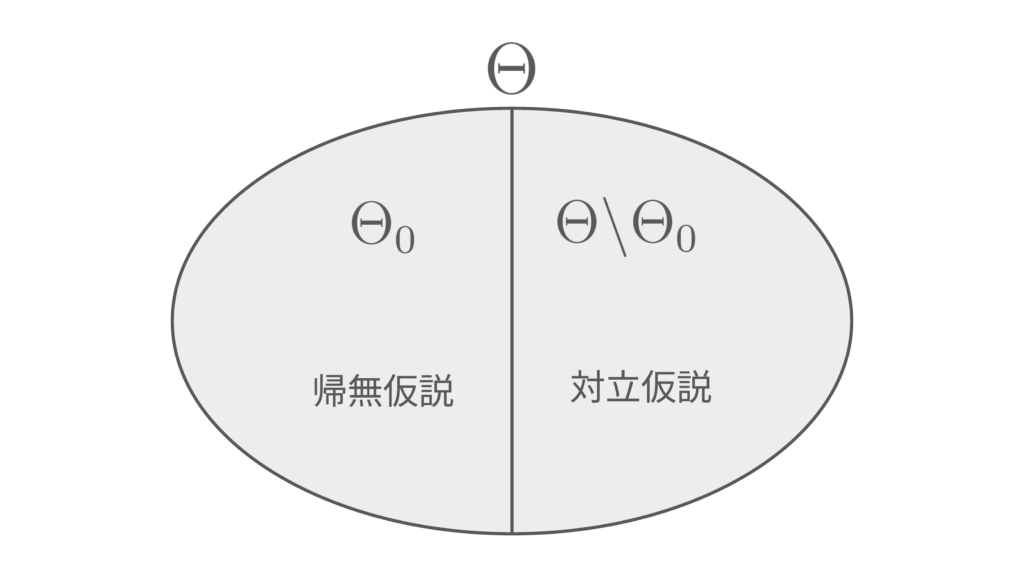
パラメータ空間\( \Theta \)は帰無仮説と対立仮説によって\( \Theta_0 \)で分割
このように設定した帰無仮説と対立仮説によってパラメータ空間\( \Theta \)(パラメータが取りうる値の範囲のこと)はすべてカバーされます。つまり、真のパラメータは帰無仮説または対立仮説のうちどちらか一方を満たすということ。

統計学における「仮説」とは、問題となる分布を決定づけるパラメータに関する「仮の説」だということ。「パラメータはこの値に等しい!」とか「パラメータはこの範囲にある!」といった主張のことですね。
単に帰無仮説(あるいは対立仮説)を主張するだけでは新たな知見を得られません。調査によって得られたデータを用いてその仮説が尤もらしいのかどうかを検証して初めて、仮説を主張した意味が生まれるのです。ですから、帰無仮説(あるいは対立仮説)が正しそうかどうかを判断すること、それが次のステップです。それが「検定」というプロセスになります。
仮説検定の「検定」
次に「検定」について深掘りしてみましょう!
これまで説明してきた帰無仮説(あるいは対立仮説)を設定した後は、この仮説が正しそうかどうかを検証したくなるはずです。そこで、実際に得られたデータ(これを確率変数の実現値という)から帰無仮説の妥当性を検討してみましょう!
得られたデータから帰無仮説の成否を判断するときは、帰無仮説は「正しそうだ」と判断するか、帰無仮説は「間違っていそうだ」と判断するかの2通りしかありません。
- 帰無仮説を受容する(fail to reject the null hypothesis)= 帰無仮説を否定できない
- 帰無仮説を棄却する(reject the null hypothesis)= 帰無仮説を否定する
「受容する」という言葉には注意が必要です。これは、帰無仮説の主張が正しいと受け入れるという意味ではありません。むしろ、得られたデータからは帰無仮説を否定する十分な証拠が得られなかったと解釈するべき。正しいかもしれないし、間違っているかもしれないし、その判断は保留にしておこう、という態度だと考えてください。

与えられたデータを根拠として帰無仮説を棄却するか否かを判断する必要がありますね!
データが与えられたとき、帰無仮説を棄却するのか否かをどのように判断するのでしょうか。そこで登場するのが検定統計量\( W(X) \)と呼ばれる関数(確率変数)です。検定統計量とは一体どのように定義されたのかと疑問を抱かれるかと思います。ですが、その定め方は後ほど説明するとして、まずは使い方を解説します。
得られたデータ\( x \)を用いて検定統計量\( W(x) \)を計算します。そして、次のように帰無仮説を「検定」します。
- データ\( x \)が棄却条件\( C \)を満たして\( W(x) \in C \)ならば帰無仮説を棄却する
- データ\( x \)が棄却条件\( C \)を満たさず\( W(x) \in C \)ならば帰無仮説を受容する
統計検定量とその条件を定めると、データごとに帰無仮説を棄却するか、受容するかが一意に決まります。ですから、標本空間を「帰無仮説を棄却するデータの集合」と「帰無仮説を受容するデータの集合」に分割できるわけです。このような帰無仮説を棄却するデータの集合を棄却域、帰無仮説を受容するデータの集合を受容域といいます。

統計学における「検定」とは、データや検定統計量などを用いて帰無仮説を棄却するか否かを判断することです。
このようにして帰無仮説(あるいは対立仮説)の成否を「検定」しますが、その判断は必ずしも正しいとは限りません。では、どのような「誤り」があるのかについて詳しく見ていきましょう!
検定統計量による「誤り」
前項で説明したように、検定統計量を用いて仮説の棄却や受容を判断したときに間違えてしまうこともあります。それは、
- 【過誤1】本来は帰無仮説\( H_0 \)が正しいにも関わらず、帰無仮説\( H_0 \)を棄却してしまう場合
- 【過誤2】本来は対立仮説\( H_1 \)が正しいにも関わらず、帰無仮説\( H_0 \)を受容してしまう場合
表現だけでは混乱してしまいそうですね。そこで、帰無仮説や対立仮説はパラメータ\( \theta \)に関する仮説でしたから、パラメータ\( \theta \)を用いて表現してみましょう!
- (過誤1)\( \theta \in \Theta_0 \)であるにも関わらず、得られたデータ\( x \)から\( \theta \notin \Theta_0 \)だと判断してしまう場合
- (過誤2)\( \theta \notin \Theta_0 \)であるにも関わらず、得られたデータ\( x \)から\( \theta \in \Theta_0 \)だと判断してしまう場合
と書き換えられます。
統計学では、【過誤1】のことを第1種の誤り、【過誤2】のことを第2種の誤りと呼ばれます。パラメータ\( \theta \)と「検定」による正誤の関係を表にまとめておきましょう!
| 帰無仮説\( H_0 \)を棄却(\( \theta \notin \Theta_0 \)と検定) | 帰無仮説\( H_0 \)を受容(\( \theta \in \Theta_0 \)と検定) | |
| 帰無仮説\( H_0 \)が正しい(\( \theta \in \Theta_0 \)) | 第1種の誤り | 正しい判断 |
| 対立仮説\( H_1 \)が正しい(\( \theta \notin \Theta_0 \)) | 正しい判断 | 第2種の誤り |

統計的な「検定」では、第1種の誤りや第2種の誤りが生じることがあります!
「検定」によって「仮説」の成否を判断するときの間違いはできる限り減らしたいものです。つまり、第1種の誤りや第2種の誤りを減らしたいということ。
だからといって、極端な検定は統計的には意味をなさないのです。たとえば、第1種の誤りを小さくできる「常に帰無仮説を受容する」という検定はどうでしょうか。あるいは、第2種の誤りを小さくできる「常に帰無仮説を棄却する」という検定はどうでしょうか。少し考えてみればわかりますが、第1種の誤りと第2種の誤りにはトレードオフの関係があることがわかります。つまり、第1種の誤りを小さくしようとすれば第2種の誤りが大きくなってしまう。逆に、第2種の誤りを小さくしようとすれば第1種の誤りが大きくなってしまうということ。
ですから、「検定」として満たすべき条件や、望ましい条件を考える必要があります。それが「検定」の有意水準や「検定」の検出力と呼ばれるもの。では、これらの基準について説明しましょう!
「有意水準\( \alpha \)」の検定
統計的な「仮説検定」の意義とは何でしょうか?
それは、データを用いて帰無仮説を棄却すること。仮説を受容したとしても、その仮説が正しいことの保証はないからです。帰無仮説を棄却することで、対立仮説を支持する根拠を得るのです。
このとき、帰無仮説を棄却するときにに生じる誤り、すなわち第1種の誤りをできる限り小さくすることが望ましいとされます。
第1種の誤りの確率に関する次の条件を満たす検定のことを、有意水準が\( \alpha \)の検定といいます。
どんな\( \theta \in \Theta_0 \)についても、第1種の誤りの確率(帰無仮説が正しいときに帰無仮説を棄却して\( \theta \in \Theta\backslash\Theta_0 \)だと検定する確率)が\( \alpha \)以下になる:
任意の\( \theta \in \Theta_0 \)について、\( \mathrm{Prob}_\theta[W(X) \in C] = \mathrm{Prob}_\theta[X \in R]\leq \alpha \)
有意水準は\( \alpha = 0.01\)や\( \alpha = 0.05\)とされることが慣習的となっています。帰無仮説を誤って棄却してしまう確率をできる限り小さく0.01や0.05に抑えましょうということ。その結果、有意水準が定められた検定で帰無仮説が棄却されると、その帰無仮説が正しくない可能性が高く、棄却の信頼性が増すのです。

帰無仮説を棄却することの信頼性を高めるために、検定に有意水準という基準を定めるわけですね。
検定の「検出力\( \beta \)」
前項では、統計的な検定において第1種の誤りの確率を有意水準以下にする意義を説明しました。有意水準によって第1種の誤りを制限した後は、第2種の誤りも小さくしたくなるもの。そこで、有意水準を満たしながらも、第2種の誤りの確率をできる限り小さくするような検定を考えてみましょう!第2種の誤りの確率を小さくするとは、
\( \beta =\)1ー(第2種の誤りの確率)
を大きくすることです。この\( \beta \)は対立仮説が正しいときに帰無仮説を棄却する確率であり、検出力\( \beta \)と呼ばれます。検出力を大きくすることは望ましい検定の条件といえるでしょう。

帰無仮説を受容することの信頼性を高めるために、検出力が高い検定のほうが望ましいということですね。
統計的な問題において「検定」方法はどのように決めればよいのでしょうか。
実は、考察する問題や仮説によって適した検定は異なります。ですから、実際に応用する場面では、問題や仮説に適した統計検定を使用することが無難でしょう。状況に合わせた方法を学び、活用していく必要があります。
まとめ
統計的仮説検定における「仮説」とは、統計的問題に関する確率変数の分布を決定づけるパラメータに関する「仮の説」のこと。その仮説は(データにより否定されることが多く)帰無仮説といい、帰無仮説とは排反な仮説を対立仮説といいます。
統計的仮説検定における「検定」とは、データから帰無仮説(あるいは対立仮説)の成否を判断すること。データによって帰無仮説を否定することを「帰無仮説を棄却する」、逆に帰無仮説を否定しないことを「帰無仮説を受容する」といいます。
実際のデータでは誤って検定してしまうことがあります。
- 【第1種の誤り】帰無仮説が正しいのに、帰無仮説を棄却してしまう過誤
- 【第2種の誤り】対立仮説が正しいのに、対立仮説を棄却してしまう過誤
得られたデータによって帰無仮説を棄却することが統計的な検定の主眼です。したがって、帰無仮説を誤って棄却するという第1種の誤りを避けたいのです。そのため、第1種の誤りの確率の上限\( \alpha \)を定め、その上限を満たす検定のことを有意水準\( \alpha \)の検定といいます。
さらに、有意水準を満たした上で第2種の誤りも極力避けたいのです。そのため、第2種の誤りを犯さない確率に相当する検出力\( \beta \)をできる限り大きくすることが望ましいのです。
統計的な問題や仮説に対する検定を定めるときには、有意水準を満たしながら、できる限り検出力を大きくすることが最も望ましいということですね。



コメント