統合情報理論ー仮定とは何か

意識を数学的に説明する統合情報理論（Integrated Information Theory；IIT）では、考察する対象が「存在性」と「構成性」を満たすことを要求します。これらの仮定によって、理論の基盤が定められます。

この記事では、具体的な例を交えながら「仮定とは何か」を解説します！

統合情報理論の仮定

まず、考察する対象の構成要素に関する「メカニズム」と「システム」について説明します。

メカニズム（mechanism）：構成要素（element）を集めたもので、他の構成要素と因果的な関係を結ぶもの。例）脳にあるニューロン・コンピュータの電子回路にある論理ゲート
システム（system）：構成要素やメカニズムをすべて集めたもの。例）脳・コンピュータ

IITでは、対象とするシステムに「存在性」と「構成性」を仮定します。

存在性（existence）：ある状態のメカニズムが存在し、システムはそのメカニズムの集合である。
構成性（composition）：低次のメカニズムを組み合わせることで、高次のメカニズムを構成できる。

つまり、すべての構成要素をグルーピングしたものがメカニズムで、そのメカニズムをグルーピングしたものがシステムとなるということです。

「存在性」とは何か？

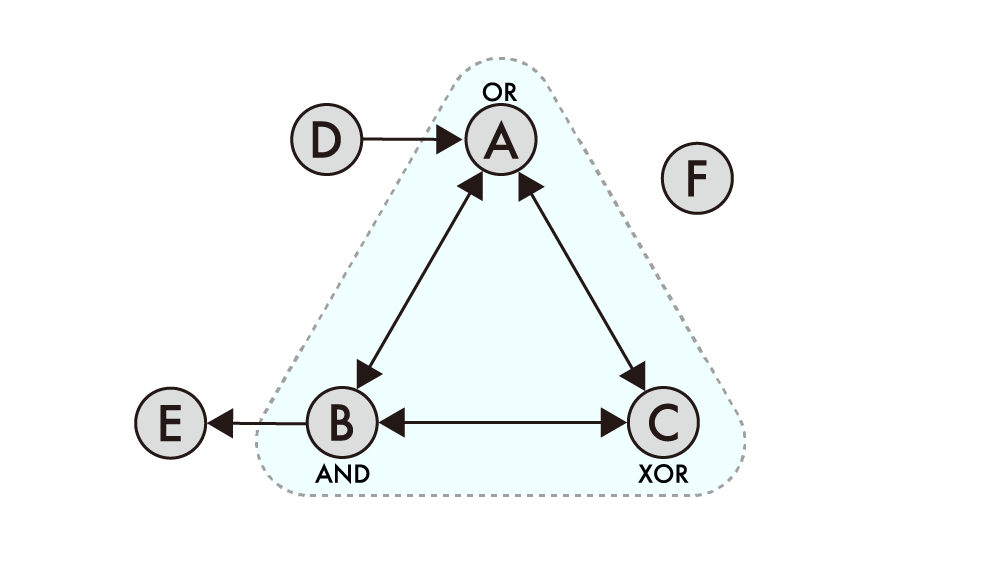
構成要素ABCDEFからなるシステムについて考えてみましょう。要素Aは単体でORゲート¹、要素Bは単体でANDゲート²、要素Cは単体でXORゲート³とします。そして、要素ABCを集めたものをメカニズムとして考察します。

すべての要素の関係を図1に示しました。離散的な各時刻でそれぞれの要素は0（off）または1（on）の状態にあります。そして、前の時刻の状態によって次の時刻の状態は決まります。たとえば、要素Aは要素BCDから入力を受けるため、それらの論理和（OR）が次の時刻の要素Aとなるわけです。

具体例を計算してみましょう。時刻\(t_0\)に要素DEFが、$$\mathrm{DEF}(t_0) = 010$$であるとします。時刻\(t_0\)に\(\mathrm{ABC}(t_0) = 100\)の場合は、次の時刻\(t_1\)に$$\mathrm{ABC}(t_1) = 001$$となります。これは、

• \(\mathrm{A}(t_1) = \mathrm{B}(t_0) \lor \mathrm{C}(t_0) \lor \mathrm{D}(t_0) = 0 \lor 0 \lor 0 = 0\)
• \(\mathrm{B}(t_1) = \mathrm{A}(t_0) \land \mathrm{C}(t_0) = 1 \land 0 = 0\)
• \(\mathrm{C}(t_1) = \mathrm{A}(t_0) \oplus \mathrm{B}(t_0) = 0 \oplus 1 = 1\)

となるからです。

このようにメカニズムABCに関するすべての状態遷移を求めれば、その遷移確率をまとめた表⁴に整理できます。

このように、すべてのメカニズムの状態は相互の依存関係によって定まり、システムとして存在しうる（存在性）のです。

「構成性」とは何か？

次に「構成性」を理解するために、先ほどと同じ要素ABCからなるメカニズムを考えます。A・B・Cはそれぞれ構成要素ですが、それ単体でメカニズムであるとみなせます。これらのメカニズムは1つの要素から構成されるため、一次メカニズム（first-order mechanism）といいます。さらに、2つの1次メカニズムを組み合わせることで二次メカニズム（second-order mechanism）、すべての1次メカニズムを組み合わせることで三次メカニズム（third-order mechanism）を構成できます。

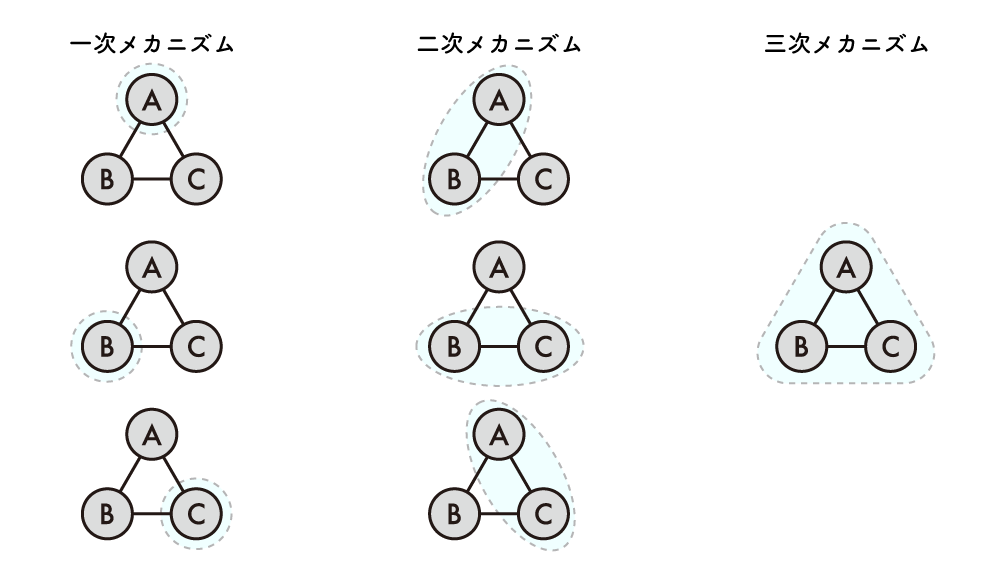
このように、低次・高次のメカニズムを組み合わせることによって、システムとして構成しうる（構成性）のです。

まとめ

• 構成要素やメカニズムを集めたものによってシステムは構成される。
• 状態が定まるメカニズムが集まりシステムが構成されることを存在性という。
• 低次のメカニズムが集まり高次のメカニズムが組み立てられることを構成性という。

脚注

1. 論理ゲートの一種であり「いずれかの入力が1であれば1を出力する」論理回路。 ↩︎
2. 論理ゲートの一種であり「すべての入力が1であれば1を出力する」論理回路。 ↩︎
3. 論理ゲートの一種であり「ひとつの入力が1であれば1を出力する」論理回路。 ↩︎
4. ある状態から別の状態へシステム（あるいはメカニズム）が遷移する確率をすべて示した表（行列）のことで、。\(\mathrm{DEF}(t_0) = 010\)として時刻\(t_1\)のTPMを求めてみましょう。メカニズムABCが要素DEFと築いている因果的な関係を表現できます。
   \[\begin{array}{c|cccccccc}
   \mathrm{ABC}(t_0) \backslash \mathrm{ABC}(t_1) & 000 & 001 & 010 & 011 & 100 & 101 & 110 & 111 \\ \hline
   000 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
   001 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
   010 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
   011 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
   100 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
   101 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
   110 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
   111 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0
   \end{array}\] ↩︎

参考文献

• Oizumi, M., Albantakis, L., & Tononi, G. (2014). From the phenomenology to the mechanisms of consciousness: integrated information theory 3.0. PLoS computational biology, 10(5), e1003588.
  https://doi.org/10.1371/journal.pcbi.1003588